The concept of plausibility functions pertains to assessing the -value of a set of null hypotheses and to plot this -value surface on the domain defined by the set of null hypotheses. The idea behind is that, if such a plausibility function is available, you can deduce from it point estimates or confidence interval estimates for parameters used to define the nulls or extract a single -value for a specific null of interest (Martin 2017; Fraser 2019; Infanger and Schmidt-Trucksäss 2019). In particular, there is another R package dedicated to plausibility functions called pvaluefunctions.
Plausibility function for the mean
null_spec <- function(y, parameters) {
map(y, ~ .x - parameters)
}
stat_functions <- list(stat_t)
stat_assignments <- list(delta = 1)
pf <- PlausibilityFunction$new(
null_spec = null_spec,
stat_functions = stat_functions,
stat_assignments = stat_assignments,
x1, x2,
seed = 1234
)
pf$set_nperms(nperms)
pf$set_point_estimate(mean(x2) - mean(x1))
pf$set_parameter_bounds(
point_estimate = pf$point_estimate,
conf_level = pf$max_conf_level
)
pf$set_grid(
parameters = pf$parameters,
npoints = ngrid_in
)
pf$set_alternative("two_tail")
pf$evaluate_grid(grid = pf$grid)
df <- rename(pf$grid, two_tail = pvalue)
pf$set_alternative("left_tail")
pf$grid$pvalue <- NULL
pf$evaluate_grid(grid = pf$grid)
df <- bind_rows(
df,
rename(pf$grid, left_tail = pvalue)
)
pf$set_alternative("right_tail")
pf$grid$pvalue <- NULL
pf$evaluate_grid(grid = pf$grid)
df <- bind_rows(
df,
rename(pf$grid, right_tail = pvalue)
)
pf$set_grid(
parameters = pf$parameters,
npoints = ngrid_out
)
df_mean <- tibble(
delta = pf$grid$delta,
two_tail = approx(df$delta, df$two_tail, delta)$y,
left_tail = approx(df$delta, df$left_tail, delta)$y,
right_tail = approx(df$delta, df$right_tail, delta)$y,
) %>%
pivot_longer(-delta)
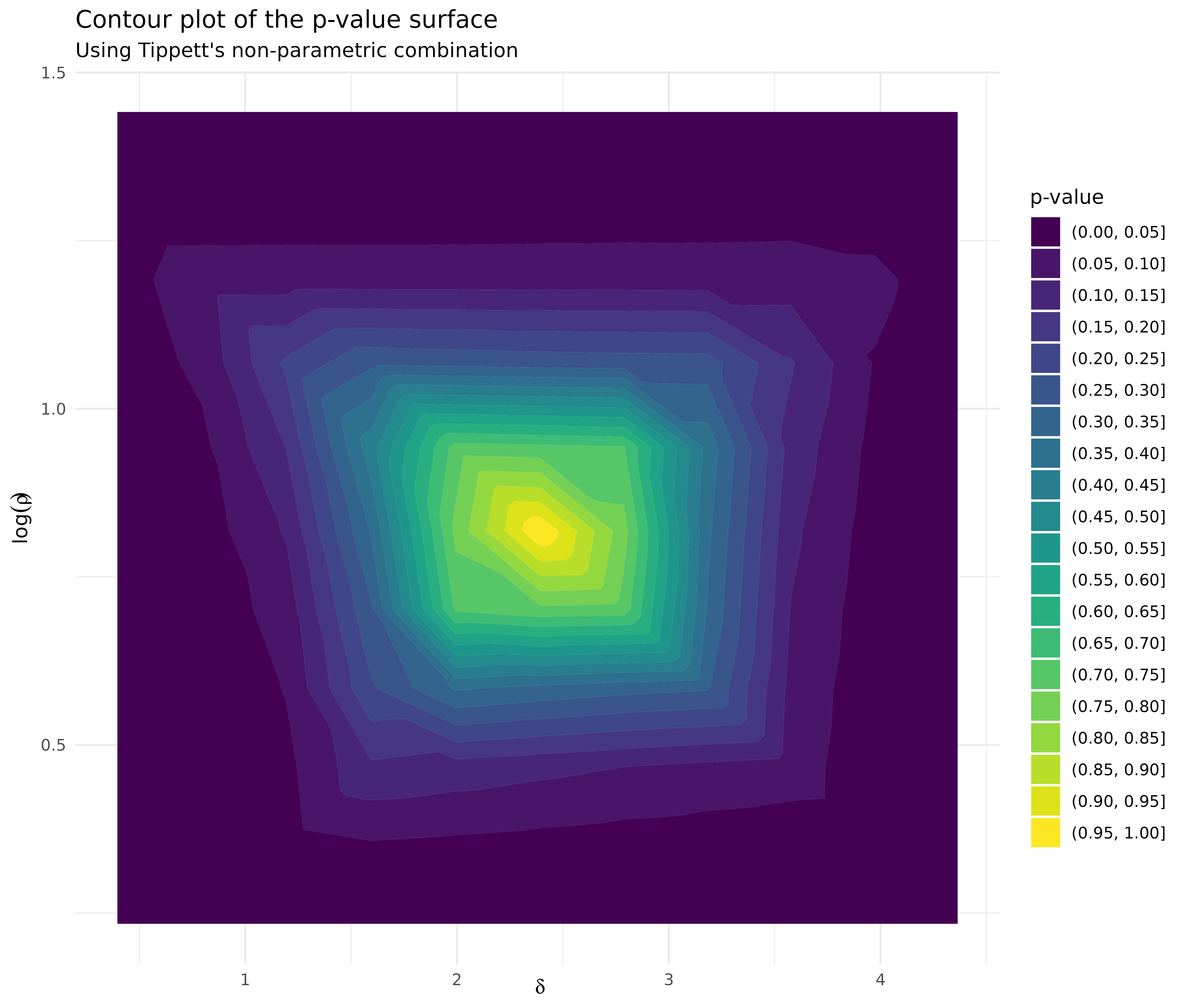
df_mean %>%
ggplot(aes(delta, value, color = name)) +
geom_line() +
labs(
title = "P-value function for the mean",
subtitle = "t-statistic",
x = expression(delta),
y = "p-value",
color = "Type"
) +
geom_hline(
yintercept = 0.05,
color = "black",
linetype = "dashed"
) +
geom_vline(
xintercept = mean(x2) - mean(x1),
color = "black"
) +
geom_vline(
xintercept = stats::t.test(x2, x1, var.equal = TRUE)$conf.int,
color = "black",
linetype = "dashed"
) +
scale_y_continuous(breaks = seq(0, 1, by = 0.05), limits = c(0, 1))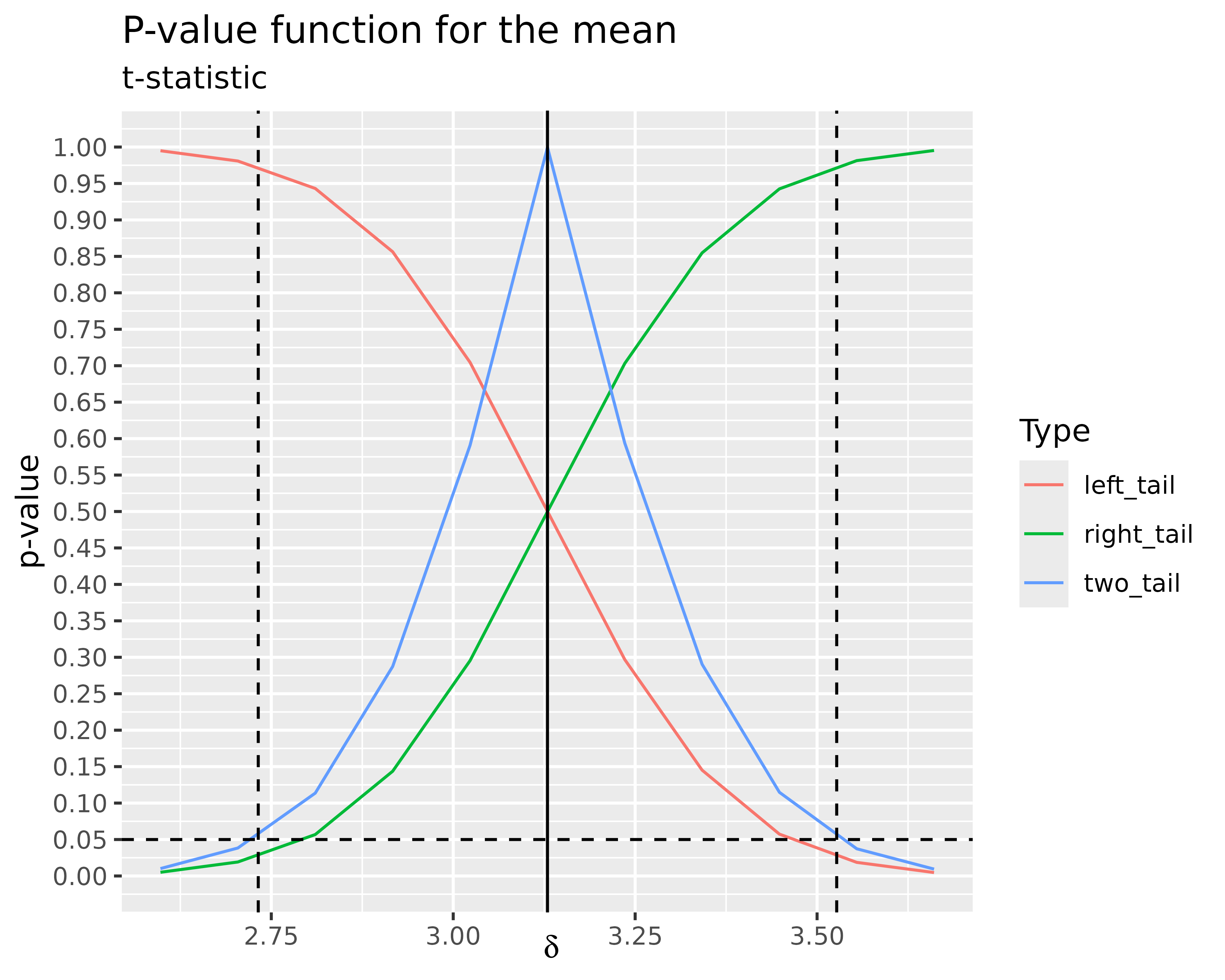
Plausibility function for the variance
null_spec <- function(y, parameters) {
map(y, ~ .x / parameters)
}
stat_functions <- list(stat_f)
stat_assignments <- list(rho = 1)
pf <- PlausibilityFunction$new(
null_spec = null_spec,
stat_functions = stat_functions,
stat_assignments = stat_assignments,
y1, y2,
seed = 1234
)
pf$set_nperms(nperms)
pf$set_point_estimate(sd(y2) / sd(y1))
pf$set_parameter_bounds(
point_estimate = pf$point_estimate,
conf_level = pf$max_conf_level
)
pf$set_grid(
parameters = pf$parameters,
npoints = ngrid_in
)
pf$set_alternative("two_tail")
pf$evaluate_grid(grid = pf$grid)
df <- rename(pf$grid, two_tail = pvalue)
pf$set_alternative("left_tail")
pf$grid$pvalue <- NULL
pf$evaluate_grid(grid = pf$grid)
df <- bind_rows(
df,
rename(pf$grid, left_tail = pvalue)
)
pf$set_alternative("right_tail")
pf$grid$pvalue <- NULL
pf$evaluate_grid(grid = pf$grid)
df <- bind_rows(
df,
rename(pf$grid, right_tail = pvalue)
)
pf$set_grid(
parameters = pf$parameters,
npoints = ngrid_out
)
df_sd <- tibble(
rho = pf$grid$rho,
two_tail = approx(df$rho, df$two_tail, rho)$y,
left_tail = approx(df$rho, df$left_tail, rho)$y,
right_tail = approx(df$rho, df$right_tail, rho)$y,
) %>%
pivot_longer(-rho)
df_sd %>%
ggplot(aes(rho, value, color = name)) +
geom_line() +
labs(
title = "P-value function for the standard deviation",
subtitle = "F-statistic",
x = expression(rho),
y = "p-value",
color = "Type"
) +
geom_hline(
yintercept = 0.05,
color = "black",
linetype = "dashed"
) +
geom_vline(
xintercept = sqrt(stats::var.test(y2, y1)$statistic),
color = "black"
) +
geom_vline(
xintercept = sqrt(stats::var.test(y2, y1)$conf.int),
color = "black",
linetype = "dashed"
) +
scale_y_continuous(breaks = seq(0, 1, by = 0.05), limits = c(0, 1))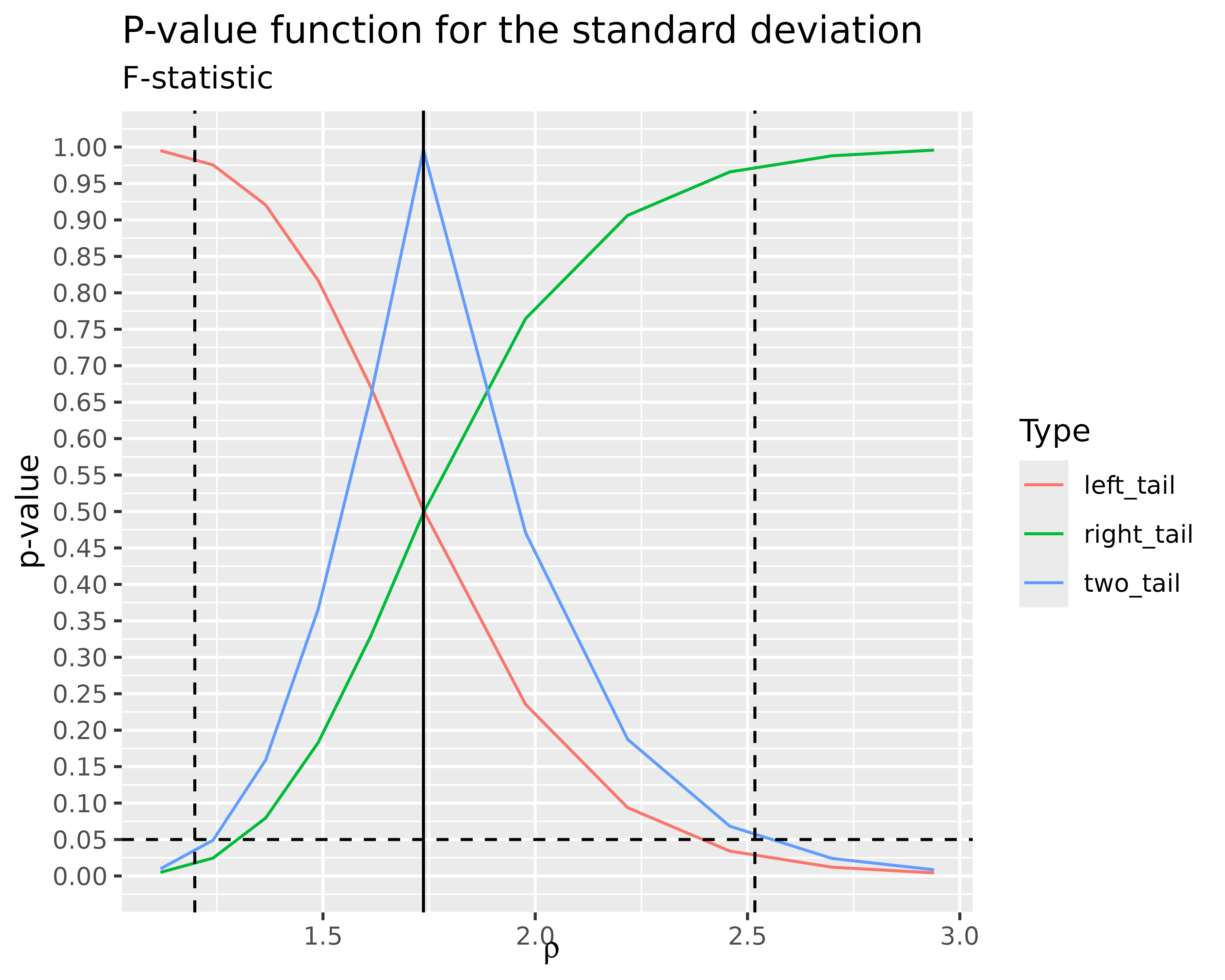
Plausibility function for both mean and variance
Assume that we have two r.v. and that differ in distribution only in their first two moments. Let and be the means of and respectively and and be the standard deviations. We can therefore write
In this case, we have
In the following example, we have and .
null_spec <- function(y, parameters) {
map(y, ~ (.x - parameters[1]) / parameters[2])
}
stat_functions <- list(stat_t, stat_f)
stat_assignments <- list(delta = 1, rho = 2)
pf <- PlausibilityFunction$new(
null_spec = null_spec,
stat_functions = stat_functions,
stat_assignments = stat_assignments,
z1, z2,
seed = 1234
)
pf$set_nperms(nperms)
pf$set_point_estimate(c(
mean(z2) - sd(z2) / sd(z1) * mean(z1),
sd(z2) / sd(z1)
))
pf$set_parameter_bounds(
point_estimate = pf$point_estimate,
conf_level = pf$max_conf_level
)
# Fisher combining function
pf$set_aggregator("fisher")
pf$set_grid(
parameters = pf$parameters,
npoints = ngrid_in
)
pf$evaluate_grid(grid = pf$grid)
grid_in <- pf$grid
pf$set_grid(
parameters = pf$parameters,
npoints = ngrid_out
)
if (requireNamespace("interp", quietly = TRUE)) {
Zout <- interp::interp(
x = grid_in$delta,
y = grid_in$log_rho,
z = grid_in$pvalue,
xo = sort(unique(pf$grid$delta)),
yo = sort(unique(pf$grid$log_rho))
)
pf$grid$pvalue <- as.numeric(Zout$z)
} else
pf$grid$pvalue <- rep(NA, nrow(pf$grid))
df_fisher <- pf$grid
# Tippett combining function
pf$set_aggregator("tippett")
pf$set_grid(
parameters = pf$parameters,
npoints = ngrid_in
)
pf$evaluate_grid(grid = pf$grid)
grid_in <- pf$grid
pf$set_grid(
parameters = pf$parameters,
npoints = ngrid_out
)
if (requireNamespace("interp", quietly = TRUE)) {
Zout <- interp::interp(
x = grid_in$delta,
y = grid_in$log_rho,
z = grid_in$pvalue,
xo = sort(unique(pf$grid$delta)),
yo = sort(unique(pf$grid$log_rho))
)
pf$grid$pvalue <- as.numeric(Zout$z)
} else
pf$grid$pvalue <- rep(NA, nrow(pf$grid))
df_tippett <- pf$grid
df_fisher %>%
ggplot(aes(delta, log_rho, z = pvalue)) +
geom_contour_filled(binwidth = 0.05) +
labs(
title = "Contour plot of the p-value surface",
subtitle = "Using Fisher's non-parametric combination",
x = expression(delta),
y = expression(log(rho)),
fill = "p-value"
) +
theme_minimal()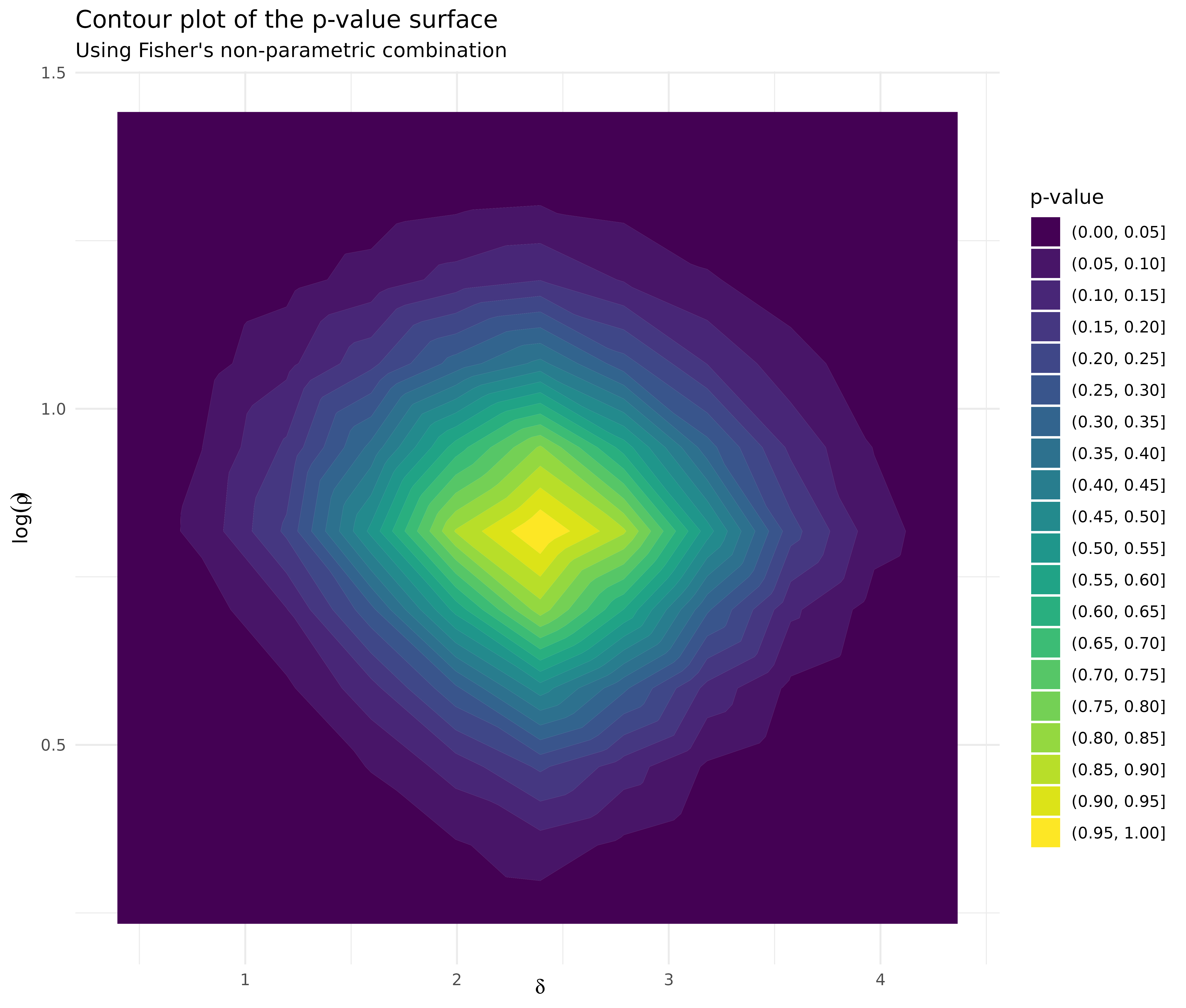
df_tippett %>%
ggplot(aes(delta, log_rho, z = pvalue)) +
geom_contour_filled(binwidth = 0.05) +
labs(
title = "Contour plot of the p-value surface",
subtitle = "Using Tippett's non-parametric combination",
x = expression(delta),
y = expression(log(rho)),
fill = "p-value"
) +
theme_minimal()